堆排序真的是面试非常容易考到的一个问题了，今天就来聊聊Heap Sort。

写这篇博客的原因是因为今天面试被问到了如何使用堆排序在一个百万数量级的数组中取出前k大的元素，可能是有点紧张，我大脑当场短路了，直接把二分搜索树和堆排序搞混了，真的是太丢人了，果不其然面试也挂了。

痛定思痛，决定自己认真的再复习和回顾一下堆排序的所有操作。

1.基本存储

首先从堆这个数据结构说起，堆可以做到入堆和出堆都是O(logn)的复杂度，平均时间上比起O(1)+O(n)这种组合要快出去很多。

首先从堆的基本形态说起，堆本质是就是一个数组，但是在存储的过程中，我们可以把它看做是一个完全二叉树:即索引为0的位置为根节点，索引为1、2的位置为根节点的子节点，下面就是一个二叉堆(Binary Heap)，对应的就是一个二叉树

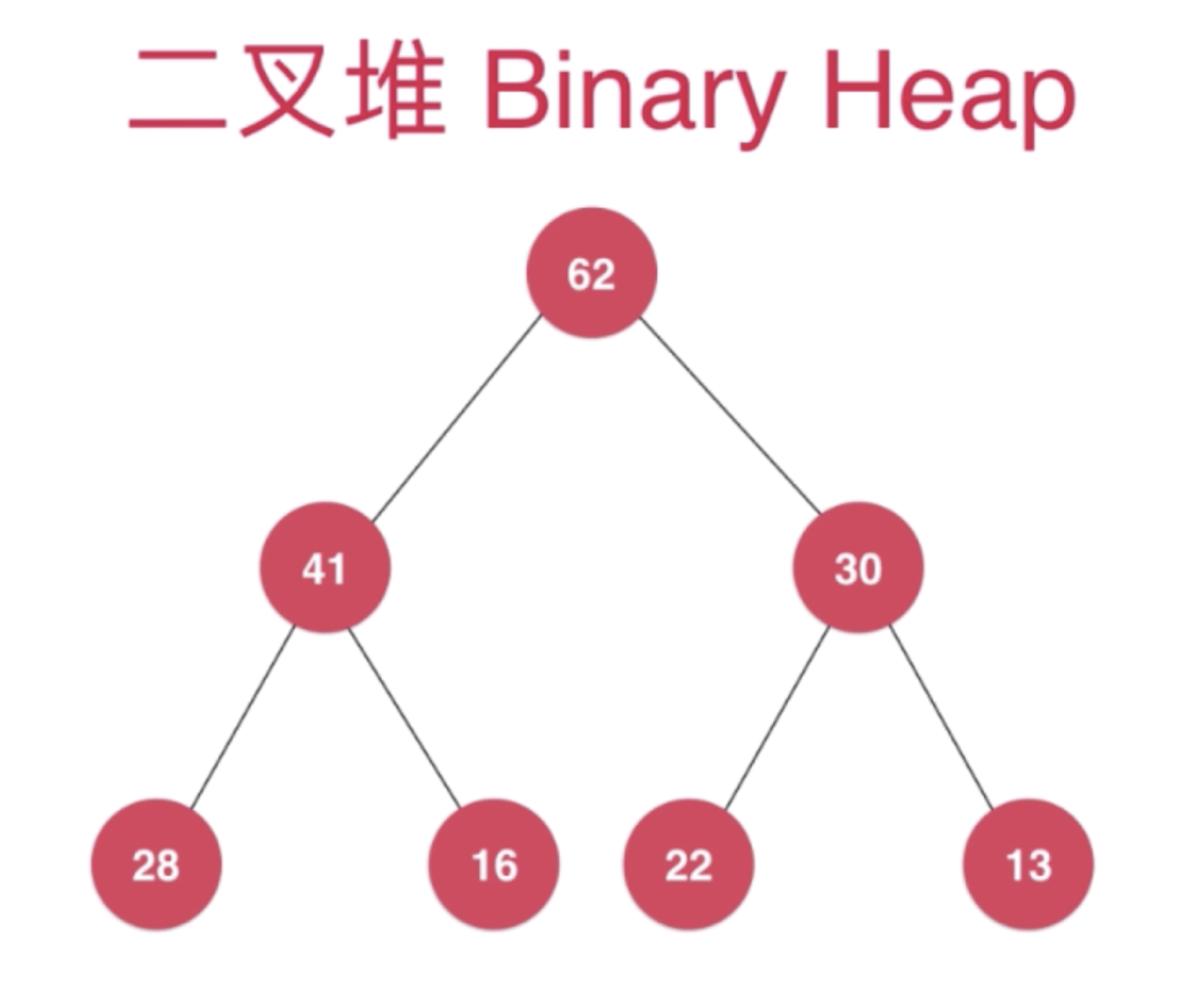
可以看到，二叉堆满足性质如下，所有子节点均小于父亲节点，即
41<62 && 30<62

并且 二叉堆是一颗完全二叉树

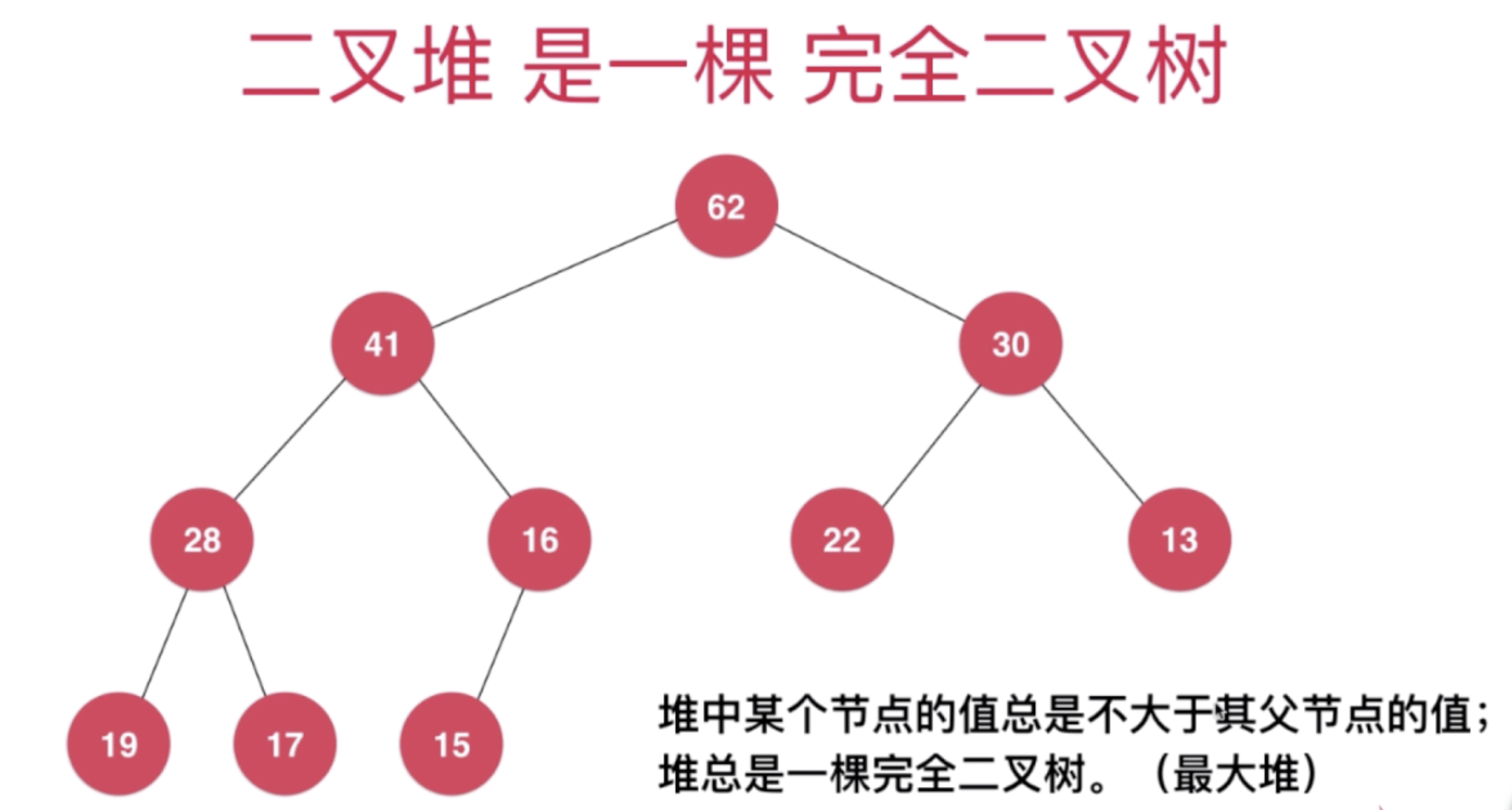
所以上图所示的堆可以在cpp中如下所存储

int arr[] = {0,62,41,30,28,16,22,13,19,17,15}

可以注意到这里index为0的元素没有使用，这是为了方便堆排序进行左右节点的计算规则。
所以这样所有的子节点和父节点就满足如下的公式

parent i = i /2;
left child i = 2 * i;
right child i = 2 * i +1;

本节对应代码：
二叉堆的建立与基本操作